4 VYTYČOVANIE PRIAMYCH A PRAVÝCH UHLOV
V geodetickej praxi sa často , vyskytujú úlohy pri ktorých treba vytýčiť uhol určitých stálych hodnôt, napr. uhol 90°{R) pri vytyčovaní kolmíc a uhol 180° (2R) pri vytyčovaní medziľahlých bodov priamky a pod.
V mnohých prípadoch sa nekladie dôraz na presnosť, ale skôr na rýchlosť vytýčenia s chybou, ktorá je pre danú úlohu prípustná. Výnimočne treba vytýčiť aj 45° uhly, ktoré sú podielom 90° uhla.4.1 VYTYČOVACIE POMÔCKY
Pomôcky na vytyčovanie uhlov stálych hodnôt (nazývané aj uhlové pomôcky) musia byť jednoduché a dostatočne presné. Môžeme ich rozdeliť na priezorové zrkadlové a hranolové [2]. V súčasnosti sa v geodetickej praxi väčšinou používajú hranolové pomôcky, priez
orové a zrkadlové pomôcky sa už používajú ojedinelo. Bližšie sú tieto pomôcky opísané [l, 2].4.1.1 Hranolové pomôcky
Hranolové
pomôcky majú trojboké alebo päťboké optické hranoly. Sú sklené telesá s presne vybrúsenými stenami: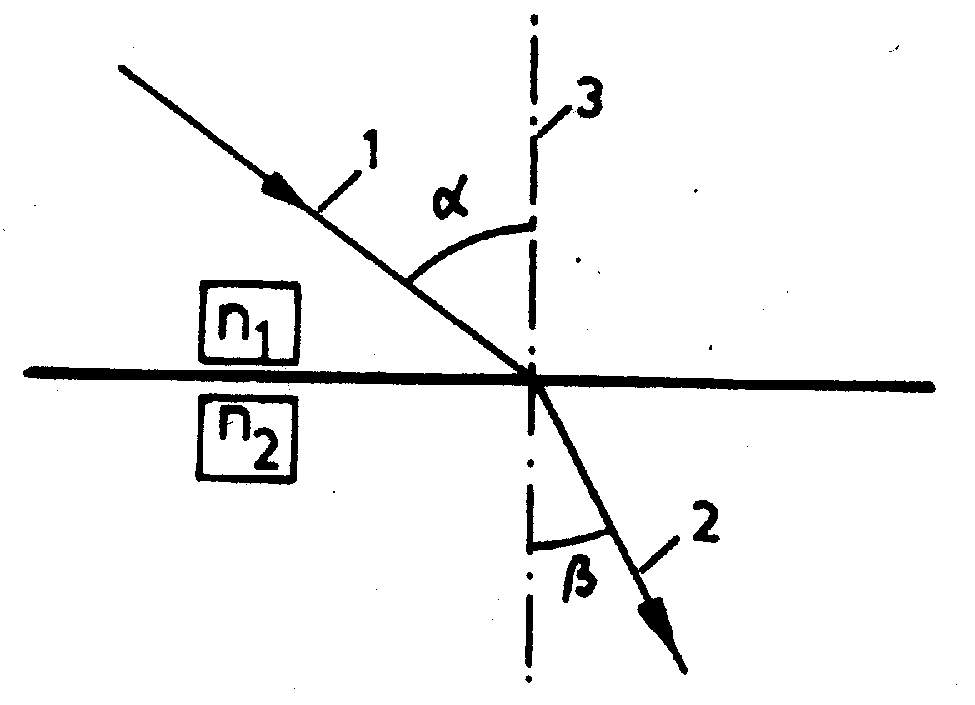
Obr. 4.1. Lom svetla
1 - dop
adajúci lúč. 2 - lomený lúč, 3 - kolmica dopaduPri hranolových pomôckach sa okrem optického zákona odrazu uplatní aj zákon lomu svetelných lúčov na rozhraní vzduchu a skla (obr. 4.l ). Lom svetla je fyzikálny jav, pri ktorom svetlo prechodom z jedného optického prostredia do druhého zmení rýchlosť, a tým aj smer. Dopadajúci lúč 1, kolmica dopadu 3 a lomený lúč 2 ležia v jednej rovine. Podiel sínusov uhla dopadu a a uhla lomu β pre obidve dané prostredia je veličina stála a rovná sa indexu lomu n (Snellov
zákon), ktorý vyjadruje známa rovnicasin α /sinβ=n (4.1)
kde α je uhol dopadu,
β - uhol lomu,
n - index lomu.
Hodnotu konštanty n určuje aj podiel rýchlosti v1 a v2 svetla alebo podiel absolútnych indexov lomu
n =sin α/sin β=
v1/v2=n2/n1 (4.2)4.1.1.1 TROJBOKÝ HRANOLČEK
Základnou hranolovou pomôckou je jednoduchý trojboký hranolček, ktorého prierezom je rovnomerný právouhlý trojuholník (obr. 4.2).
Preponová stena hranolčeka je amalgámová a pôsobí ako zrkadlo, ktoré dáva úplný odraz. Odvesné steny hranolčeka sú číre. Hranolček je upevnený v kovovej objímke. Na spodnej časti objímky je pripevnené
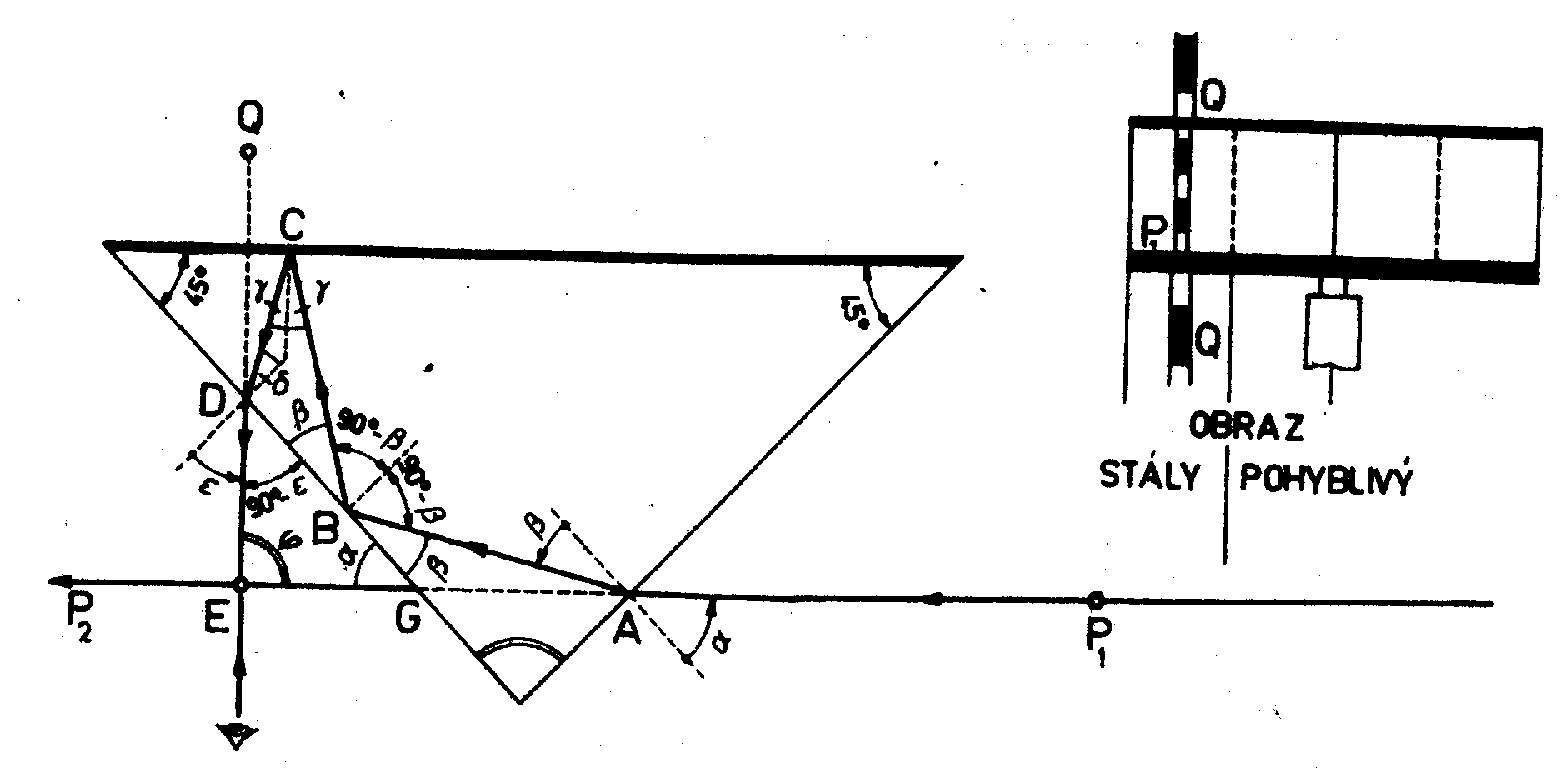
Obr. 4.2. Chod svetelných lúčov v trojbokom hranolčeku
držadlo s háčikom na olovničku. Hranolčekom možno vytyčovať pravý
uhol.V zornom poli hranolčeka (obr. 4.2 vpravo) vidno jednak svetlý obraz, ale pri otáčaní hranolčeka okolo zvislej osi pohyblivý obraz, pri ktorom sa svetelný lúč odráža iba raz od preponovej steny, a jednak menej svetlý obraz a na otáčanie hranolčeka okolo zvislej osi nereagujúci stály obraz, ktorého poloha sa nemení. Na vytyčovanie kolmice môžeme použiť iba stály obraz. Stály obraz sa objaví pri okraji hranolčeka, keď preponová stena je približne rovnobežná s priamkou P1 P2, na ktorú v bode E chceme vy
týčiť kolmicu. Pri stálom obraze sa svetelný lúč odráža prvý raz od odvesnej steny a druhý raz od odvesnej steny a tretí raz od preponovej steny.Dráha svetelného lúča P1, A, B, C, D a E je pri jeho dvojitom odraze v hranolčeku znázornená na obr. 4.2 vľavo, podľa ktorého sa odvodí aj dôkaz, že lúč vychádzajúci z hranolčeka zviera s lúčom vchádzajúcim do hranolčeka uhol
j = 90°
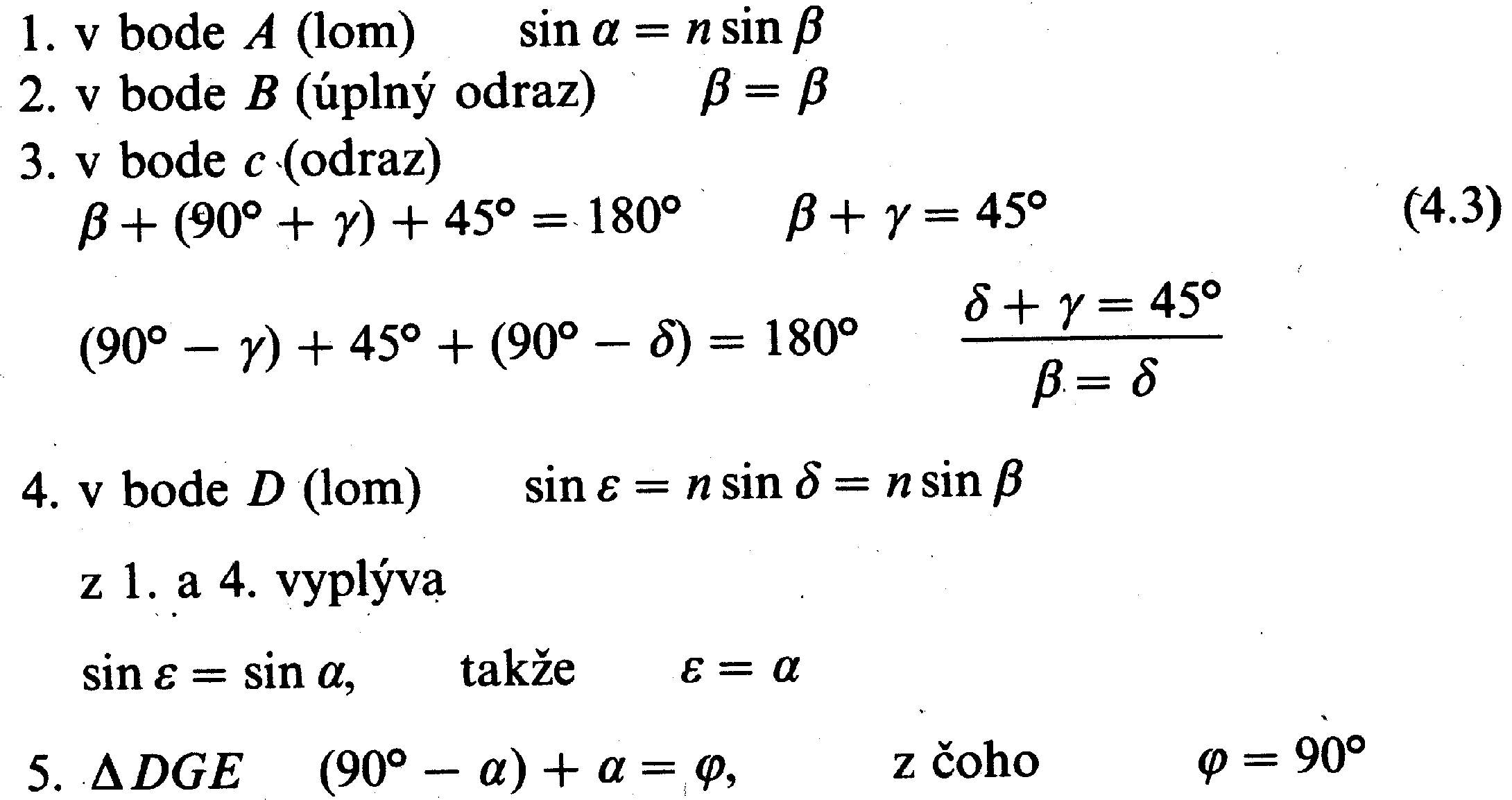
Ťrojboký hranolček pri vytyčovaní kolmice treba držať v ruke zvisle (na bode E, v ktorom chceme vytýčiť kolmicu) pred jedným okom tak aby preponová stena bola približne rovnobežná s meračskoú priamkou P1 P2 (obr. 4.2). V sklenom obraze sa na prepone objaví výtyčka z bodu Pl . Hranolčekom posúvame v smere priamky
P1 a P2 tak, aby sa nad a pod hranolčekom objavila výtyčka Q stavaná na mieste kolmice.4.1.1.2 PÄŤBOKÝ HRANOLČEK
V geodetickej praxi na vytyčovanie uhlov so stálou hodnotou najviac rozšíŕený päťboký hranolček - pentagón, ktorý oproti trojbokému hranolčeku má prednosti v tom, že má väčšié zorné pole a poskytuje . jasnejšie obrazy a priesečník na seba kolmých smerov je vnútri hranolčeka. Schéma päťbokého hranolčeka a svetelných lúčov je na obr. 4.3.
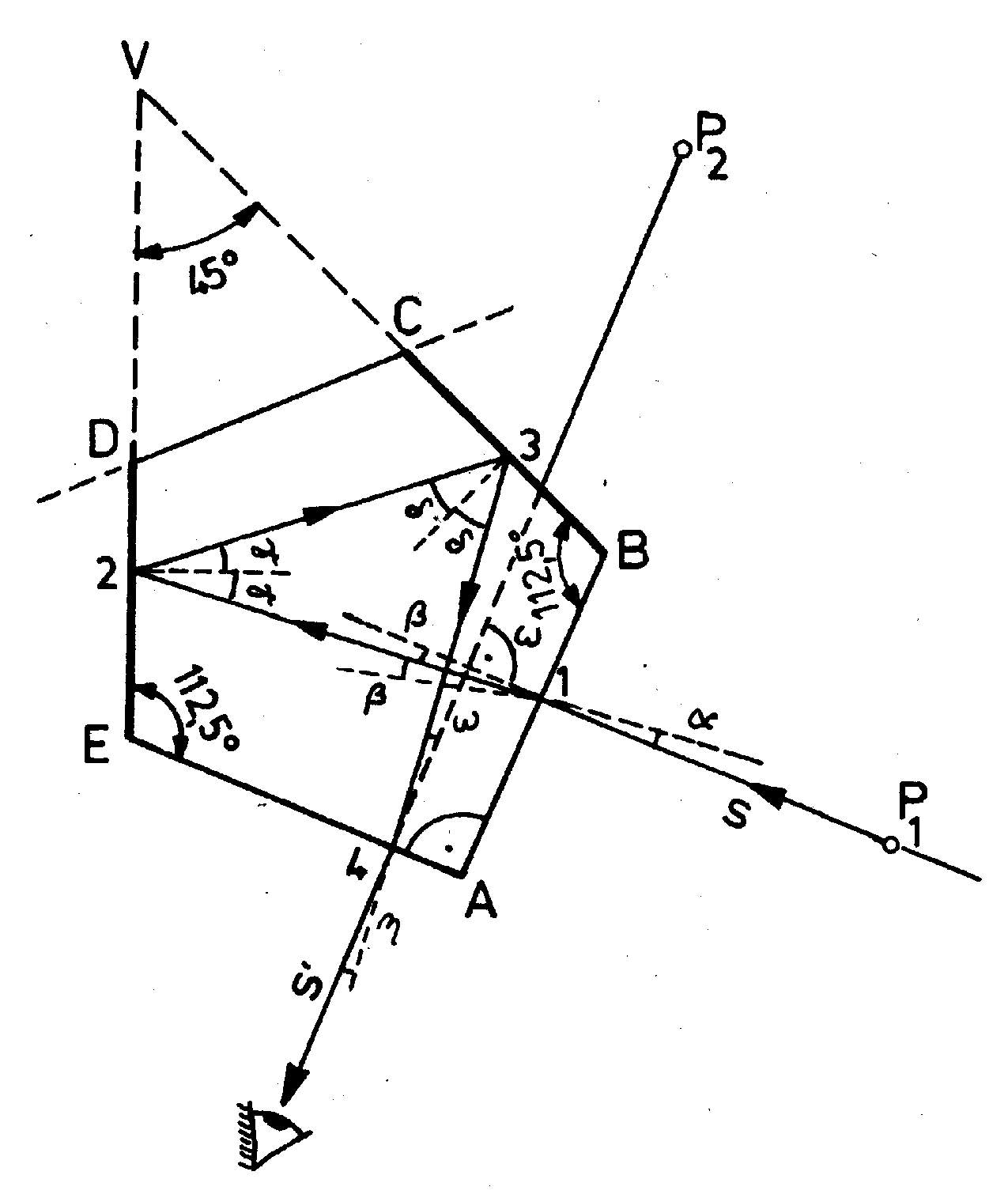
Obr. 4.3. Chod svetelných lúčov v päťbokom hranolčeku
Jeh
o prierezom je päťuholník súmerný podra osi AV s uhlom R vo vrchole A, ktorý vznikol zo štvoruholníka obrúsením skleného materiálu pri bode V. Steny BC a DE päťbokého hranola sú amalgámové a zvierajú spolu uhol 45°. Podľa obr. 4.3 možno dokázať, že svetelný lúč s, prichádzajúci z bodu Pl do hranolčeka, sa odrazom o obidve zrkadliace plochy odchýli o uhol 90°. Lúč s dopadajúci z bodu Pl na číru stenu v bode 1 sa láme ku kolmici, v bodoch 2 a 3 sa odráža, v bode 4 sa láme od kolmice a v smere s' prichádza do oka merača. Dôkaz, že lúč s' zviera s lúčom s uhol 90° vyplýva z obr. 4.3.
1. v bodé 1 (lom) sin a = n sin /3 ~. v bode 2 a 3 (odraz)
(90° + /3) + 2 y + (90° + b~ + 112°30' + 90° = 360° ° z čoho ~i + 2 y + ~ = 67°30'
3. v bode 4 (lom) sin ri = n sin E Z porovnania 1. ~a 3. vyplýva :
sin a = n sin ~i = n sin E = sin r~ a = ri Pre uhol v ~riesečníku lúčov s a s' platí : w = a + 90° - ri, čiže ~ = 90°
4.1.1.3 DVOJITÝ PÄŤBOKÝ HRANOLČEK
Dvojitý päťboký hranolček (obr. 4.4) umožňuje súčasné vytýčenie priameho aj pravého uhla. Skladá sa z dvoch päťbokých hranolčekov navzájom pootočených o pravý uhol, ktoré sú pripevnené nad sebou

Obr. 4.4. Dvojitý päťboký hranolček firmy Wild s háčikom v puzdre s držadlom. Pohyb svetelných lúčov v dvojitom hranolčeku je znázorn
ený na obr. 4.5.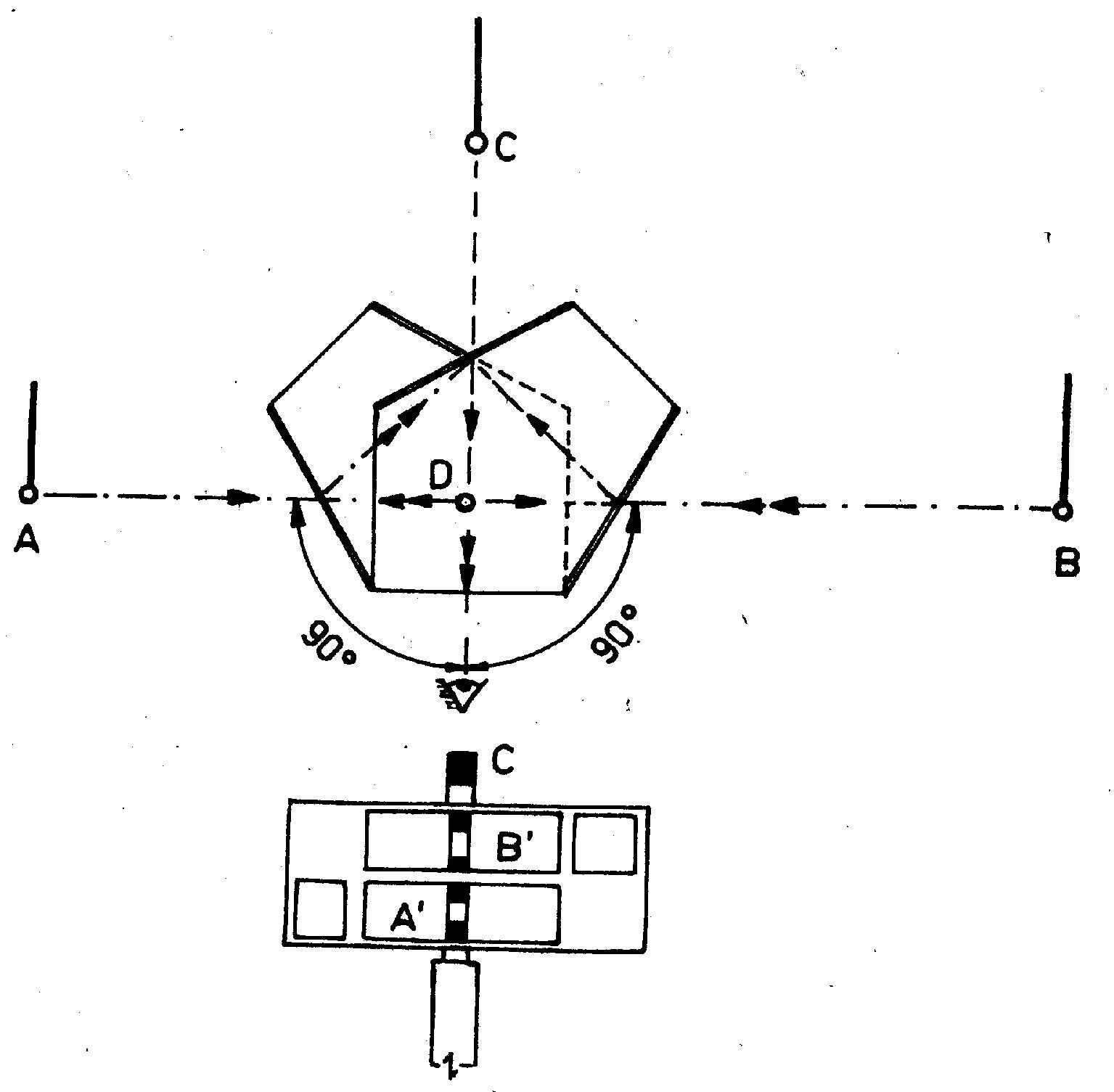
Obr. 4.5. Chod svetelných lúčov v dvojitom pentagóne
4.2 PRAKTICKÉ POUŽITIE HRANOLČEKOV
V súčasnosti sa v praxi najčastejšie na vytyčovanie uhlov stálych hodnôt používajú jednoduché alebo dvojité hranolčeky (pentagóny). Pri vytyčovaní kolmíc pentagónom sa na koncových bodoch priamky zvislo postavia výtyčky A a B (obr. 4.6) a v mieste, kde chceme vytýčiť kolmicu, na priamke vyhladáme bod D alebo F, nad ktorým podržíme pentagón tak (obr. 4.7), aby záves olovnice na držadle mieril presne na
bod D, prip. F, a aby jedna stena pentagónu bola približne rovnobežná s priamkou AB. Pohľadom cez obraz výtyčky A' alebo B' (obr. 4.6) a v jeho predĺžení nasmerujeme pomocníka s výtyčkou do bodu C, príp. E. V okamihu, keď sa výtyčka postavená na bode C objaví presne nad obrazom výtyčky A'. Obdobne je to pri vytýčení kolmice na bode E. Do takto vytýčených bodov zarazíme kolík na označenie päty kolmice.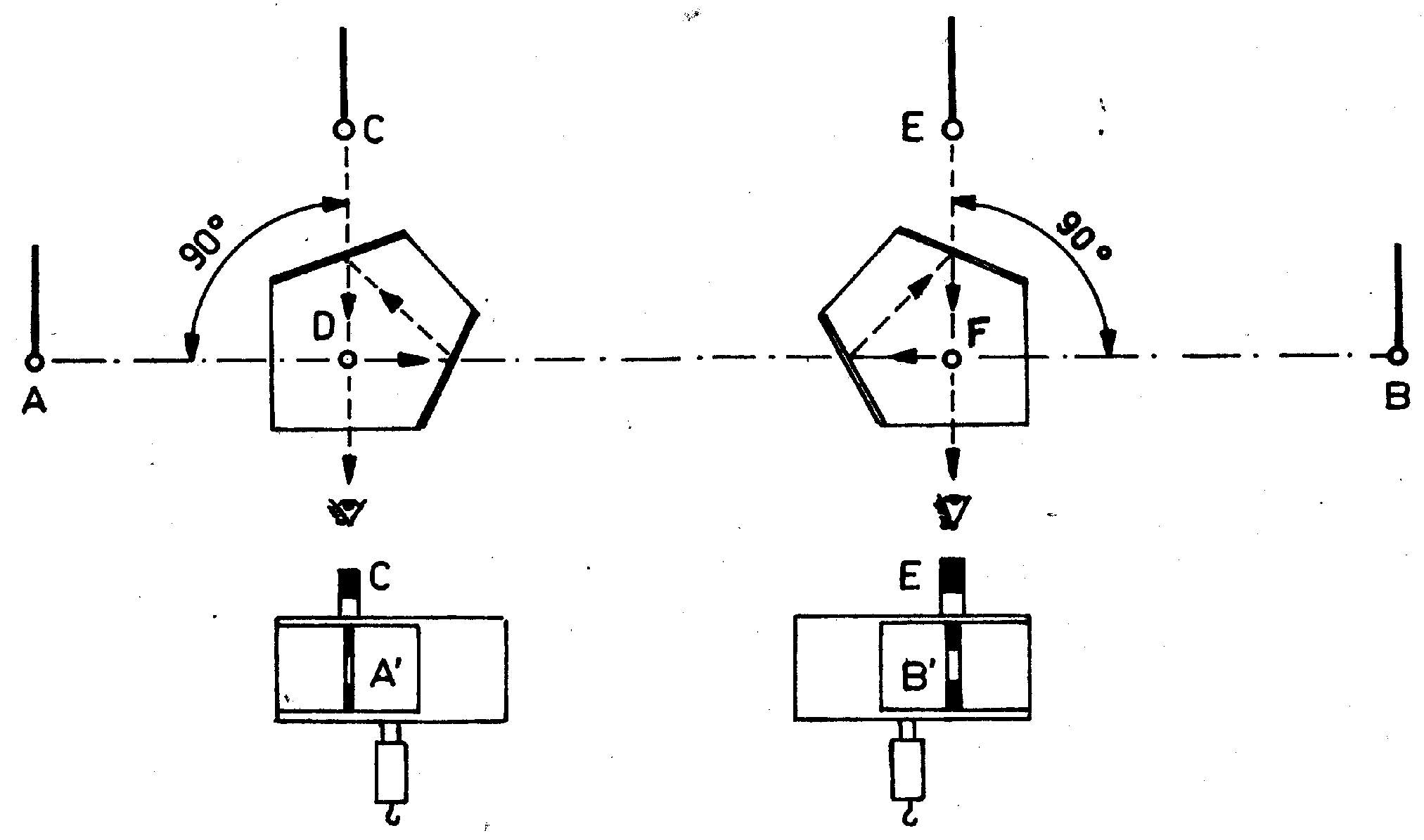
Obr. 4.6. Vytýčenie kolmice pentagónom
Postup vytýčenia kolmice dvojitým pentagónom je obdobný ako pri jednoduchom pentagóne, rozdiel je iba v tom, že v obraze pentagónu sa nad sebou objavia obidve výtyčky, t.j. z bodu A a bodu B (obr. 4.5). Vytyčovaná kolmica C je v predĺžení nad obrazom výtyčiek v pentagóne.
Pri vytyčovaní kolmice v bode C (obr. 4.7) alebo pri spustení kolmice z bodu D (obr. 4.7b) postupujeme tak, že najprv vykonávame operácie v smere 1, a potom v smere 2.
Uhly stálych hodnôt sa vytyčujú aj ďalšími uhlovými pomôckami, napr. dvojitým pentagónom firmy Zeiss s novšou konštrukciou s tyčovou olovnicou (obr. 4.8). Pri používaní sa podstatne zvyšuje presnosť pri vytyčovaní pravého uhla a urýchruje práce tým, že merača nezdržuje ustarovanie polohy olovnice, najmä pri veternom počasí do smeru priamky a pod.
Presnosť hranolových uhlových pomôcok na vytyčovanie priamych a pravých uhlov, pri vytyčovaní kolmice dlhej 20 m je asi ± 20. mm, to znamená 2' v rovinatom teréne. V hornatom teréne a pri kolmiciach dlhších ako 20 m sa uvedená presnosť znižuje.
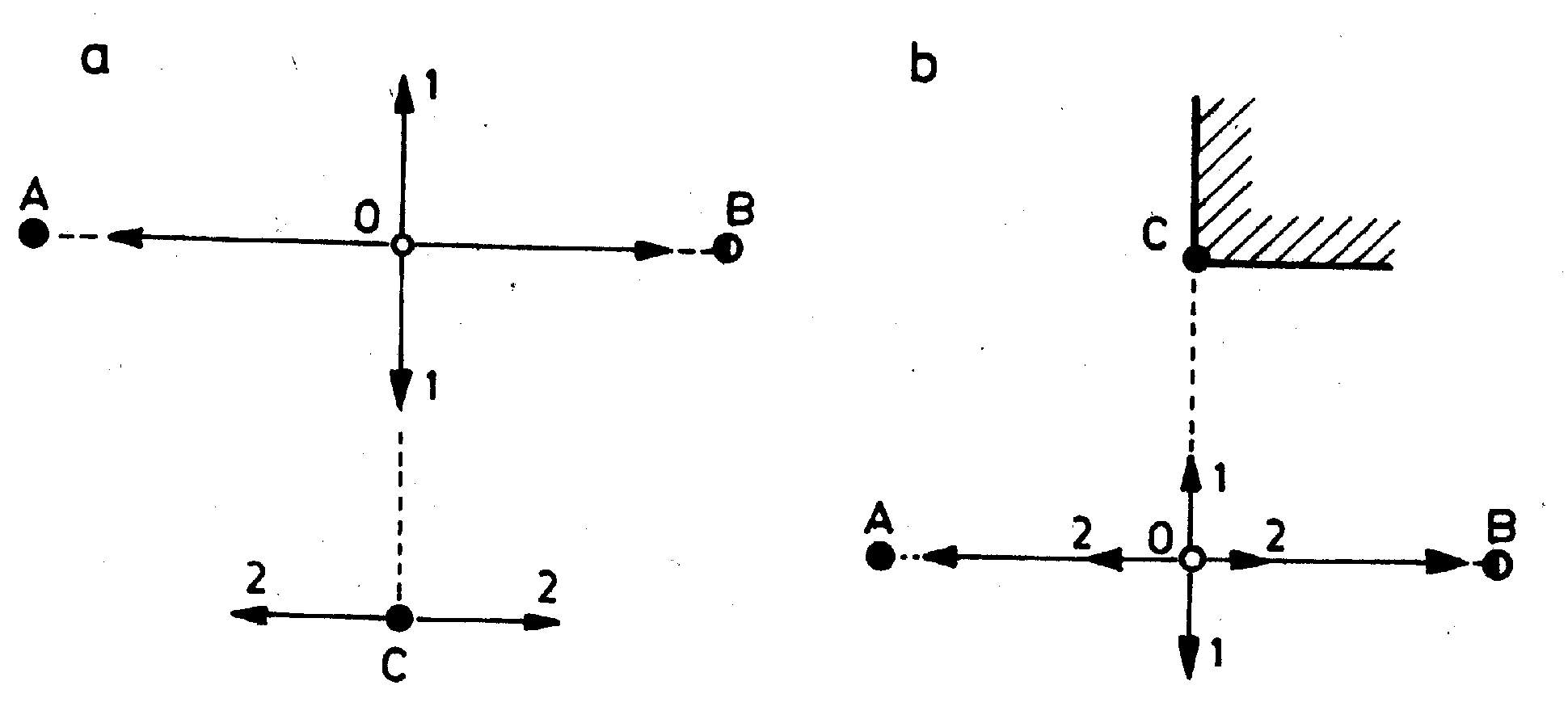
Obr. 4.7. Vytýčenie a spustenie kolmice pentagóno
m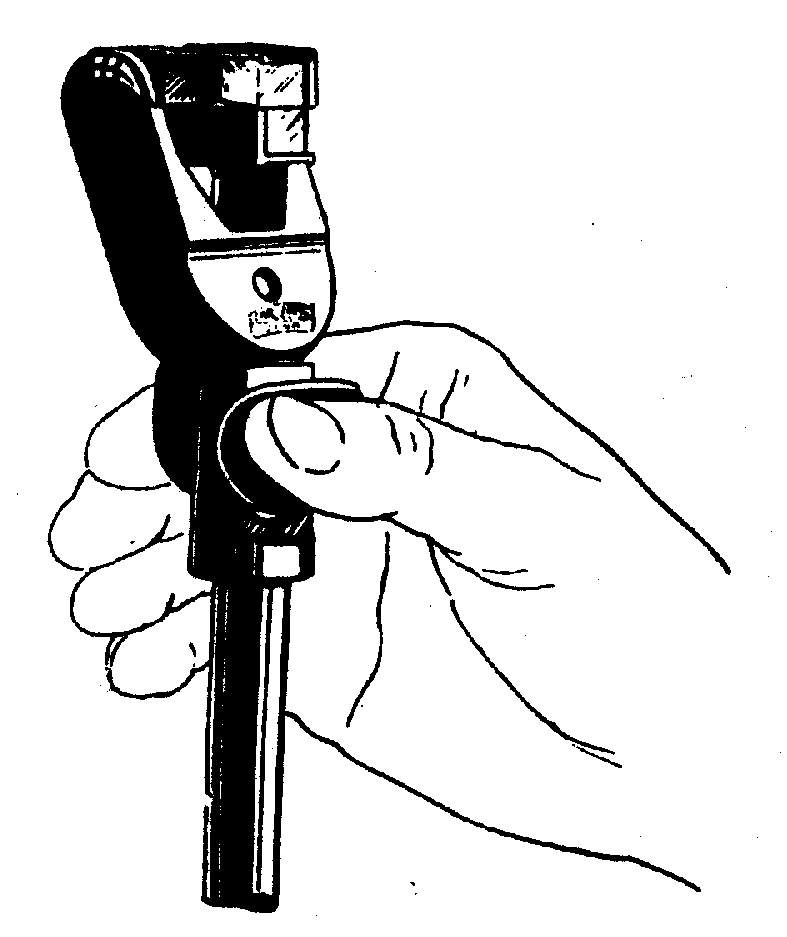
Obr. 4.8. Dvojitý pentagón firmy Zeiss s vytyčovacou olovnicou
Kontrolné otázky:
l. Aké pomôcky na vytyčovanie uhlov so stálymi hodnotami poznáte?
2. Čo tvorí princíp hranolových pomôcok na vytýčovanie uhlov so stálymi hodnotami?
3. Aký je rozdiel medzi j
ednoduchým a dvojitým hranolčekom?