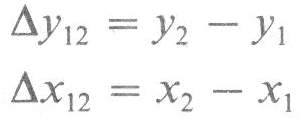
2 GEODETICKÉ METÓDY URČOVANIA POLOHY BODOV
Pri určovaní polohy bodov jednoduchých geodetických sietí, pri riešení ktorých sa využívajú geometrické obrazce, napr. trojuholníky, môžeme na výpočet ich súradníc využiť všeobecnú sínusovú vetu.
Pri zložitejších úlohách sa na určovanie vzájomnej polohy bodov používajú metódy riešenia pravouhlých a polárnych súradníc vo vhodne zvolenej súradnicovej sústave. Súradnicový spôsob výpočtu umožňuje prehľadne riešiť aj tie najzložitejšie úlohy, pričom možno kontrolovať výpočty a grafické zobrazenie polohy príslušných bodov. Pri výpočtoch sa obvykle uplatnia obidva typy súradníc, t.j. pravouhlé a polárne súradnice. Postup výpočtu vychádza z pravouhlých
súradníc bodov, z ktorých sa vypočítajú smerníky a dĺžky strán, a potom premenou (transformáciou) z pravouhlých súradníc sa vypočítajú polárne súradnice a naopak.2.1 PRAVOUHLÁ ROVINNÁ SÚRADNICOVÁ SÚSTAVA
Polohu začiatku a kladný smer osi x možno zvoliť ľubovoľne. Takáto sieť sa nazýva lokálna alebo miestna. Kladný smer osi y sa určí otočením smeru osi x o 90° (R) v smere pohybu hodinových ručičiek. V geodézii sa v rovnakom smere číslujú aj uhlomerné stupnice teodolitov. V analytickej geometrii je kladný
smer narastania uhla v opačnom smere. Tieto súradnicové sústavy (v geodetickej a analytickej geometrii) majú spoločné to, že jednotlivé kvadranty postupujú podľa kladného zmyslu, čiže všetky vety a poučky z matematiky možno aplikovať aj v geodézii.V súčasnosti sa v ČSFR v základnom a podrobnom geodetickom bodovom poli poloha každého bodu vyjadruje pravouhlými súradnicami x a y v súradnicovom systéme S-JTSK (systém jednotnej trigonometrickej siete katastrálnej).
2.2 ZÁKLADNÉ GEODETICKÉ ÚLOHY V BODOVOM POLI
Základným obrazcom pre geodetické výpočty je rajón (obr. 2.1 ). Rajón určuje meraný bod smerom a dĺžkou strany d, teda polárnymi súradnicami. Pomocou týchto prvkov sa od známych bodov S a A vypočítajú polárne súradnice meraného bodu B.
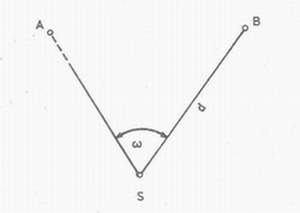
Obr. 2.1. Rajón
- uhol určovaného smeru, d - dĺžka
2.2.1 Výpočet smerníka a dĺžky strany
Keď sú známe dva body P1 a P2 pravouhlými súradnicami y1 , x1 a y2, x2, smerníkom strany d12 je uhol j = Q12 o ktorý je táto strana odklonená od rovnobežky s kladným smerom osi x - uvažuje sa v smere pohybu hodinových ručičiek (obr. 2.2).
Pri každej strane rozlišujeme dva smerníky: d
12 - smerník z bodu P1 na bod P2,d 21 - smerník z bodu P2 na bod P1.
Prvý index vždy označuje bod, z ktorého smerník vychádza. Uvedená definícia smerníka, ako aj vzorce z toho odvodené, platia pre každú súradnicovú ľubovoľne orientovanú sústavu, keď sa dodržia uvedené zásady, t.j. že kladná os y je odchýlená od kladnej osi x o 90° (R) v smere pohybu hodinových ručičiek.
Smerník d
12 vypočítame z pravouhlého trojuholníka P1QP2(obr. 2.2), ktorého odvesnami sú súradnicové rozdiely y∆l2 a ∆xl2, pričom platí
Smerník d 12 určíme výpočtom ako tangens uhla (2.2)Obr. 2.2. Výpočet smerníka a dĺžky stranyPodľa obr. 2.2 sa smerník d
21 v bode P2 líši od smerníka v bode P1 d 12 o 2R, tedaVzťah (2.2) platí pre prípad na obr. 2.2, keď y2 > y1 a x2 > x1 . V danom prípade obidva súradnicové rozdiely ∆l2 a ∆l2 sú kladné. Strana d12 je v I. kvadrante. Určovaný smerník je v tomto prípade totožný s tabuľkovým uhlom j . Výpočet tabuľkového uhla, ktorý je vždy menší ako R (90°), vykoná sa podľa
Vzorc
a (2.2), pričom sa použijú absolútne hodnoty ∆l2 a 012.Smerník a12 môže však nadobudnúť hodnoty v rozhraní 0° až 360°
a môže teda patriť do ktoréhokoľvek zo štyroch kvadrantov I. až IV. (obr. 2.3 ). Preto pri výpočte smerníka treba brat zreteľ aj na znamienko jeho sínusu a kosínusu, ktoré ovplyvňuje znamienko súradnicových rozdielov. Na obr. 2.3 sú znázornené štyri rozličné prípady, keď strana d12 je v I. až IV. kvadrante. Hodnoty smerníkov pre všetky kvadranty, určené podľa znamienok súradnicových rozdie
lov, sú v tab. 2.1.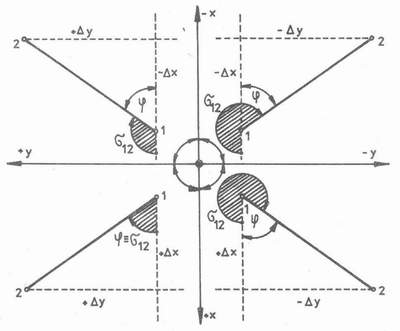
Obr. 2.3. Smerník strany v rozličných kvadrantoch
Tabuľka 2.1
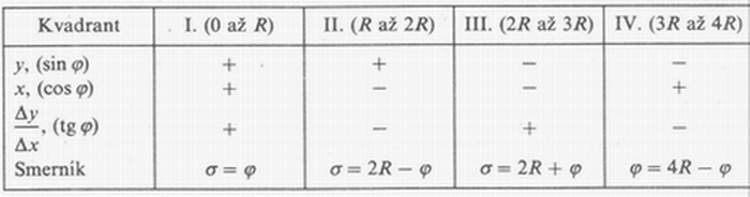
Hodnoty smerníka a tabuľkového uhla v rozličných kvadrantoch
Pretože pri mnohých geodetických výpočtoch sa vychádza zo smerníka, treba kontrolovať jeho výpočet 45-stupňovou (50 grádovou) skúškou, t.j. výpočtom smerníka (d
12 + 45°), prípadne (d 12 + SOg) podľa vzorca
ktory vypliva zo vztahu
Obidva výsledky vypočítané podľa rovnice (2.6) nie sú vždy rovnako presné. Presnejšia je tá hodnota d12 ktorá sa vypočíta z väčšieho súradnicového rozdielu (Lalandovo pravidlo). Druhá hodnota, vypočítaná z menšieho súradnicového rozdielu, má iba kontrolný význam a pri ďalšom výpočte sa neberie do úvahy.
Dĺžka strany d12 sa môže vypočítať aj zo súradníc daných bodov P1 a P2 Pytagorovou vetou podľa vzorca
Použije vtedy, keď nepotrebujeme určiť aj smerník.
2.2.2 Určenie súradníc bodu z dĺžky strany a smerníka .
Pri určení súradníc bodu zo smerníka a dĺžky strany ide o prevod polárnych súradníc na pravouhlé
súradnice.Dané sú dva body súradnicami P1 ( y1 , x1 ), P2 ( y2, x2). Máme určiť súradnice bodu P3 ( y3 , x3 ). Z jedného z daných bodov (napr. P1 ) odmeriame priamo vzdialenosť P1P3 = d13 a vrcholový uhol w
1 strán d12 a d13 (obr. 2.4a).Z obr. 2.4a vyplýva
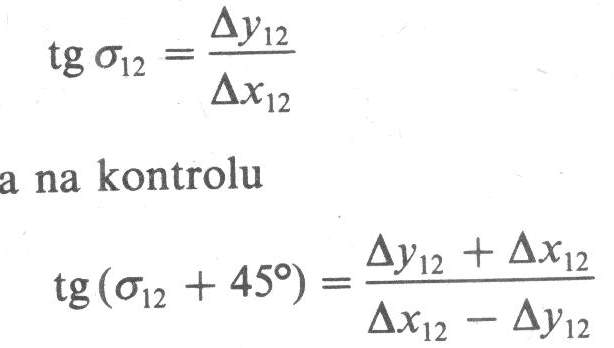
čím sme vypočítali smerník strany d12. Pre smerník d
13z obr. 2.4b dostanemeObr. 2.4: Určenie súradníc bodu rajónom
Opačnou úlohou je výpočet polárnyc
h súradníc z pravouhlých súradníc dvoch daných bodov P1 ( y1,x1 ), P2 ( y2 , x2 ). Smerník d z vypočítame podobne ako v predchádzajúcom prípade, čiže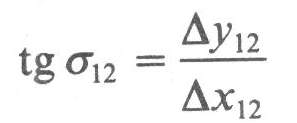
Pre dĺžku strany dostaneme
2.3 URČENIE PRAVOUHLÝCH SÚRADNÍC Z MERANÝCH UHLOV A DĹŽOK
Úloha sa vyskytuje najmä pri podrobnom mapovaní polohopisu metódou pravouhlých súradníc. Sieť meračských priamok tvoria nielen polygónové strany, ale aj spojnice meračských bodov P, ľubovoľne zvolených na polygónových stranách.
2.3.1 Výpočet súradníc bodov na meračskej priamke Poznáme súradnice koncových bodov meračskej priamky P( yp, xp), K(yK, xK) a merané dĺžky di¢ od bodu P k určovaným bodom a ku koncovému bodu, t.j. ich staničenia (obr. 2.5 ).
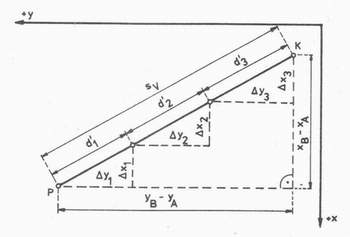
Obr. 2.5. K výpočtu súradníc bodov na meračskej priamke
Zo súradníc začiatočného a koncového bodu meračskej priamky vypočítame podľa vzorca (2.2) smerník strany PK
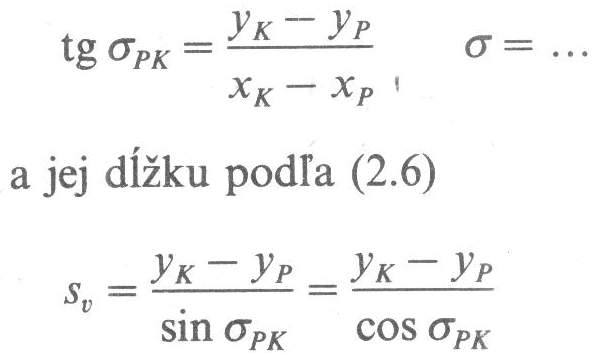
Dĺžku sv môžeme vypočítať aj pomocou pytagorovej vety podľa vzorca
Vypočítaná vzdialenosť sv sa musí rovnať meranej vzdialenosti dm
t.j. musí byť rovnaká ako súčet úsekov dm = d1¢
+ d2¢ + d3¢ . Dovolený malý rozdiel Os = sv - dm nesmie byť väčší ako dovolená odchýlka. Podľa smerníc pre mapovanie pre prípustnú odchýlku Os platíkde d je hodnota meranej dĺžky (m).
Po zistení, že odchýlka Os nie je väčšia ako dovolená odchýlka ∆s (Os <= ∆s ), začne sa s výpočtom súradnicových rozdielov. Pretože opravené dĺžky d1, d2, d3, ... musia vyhovovať úmerám
možno súradnicové rozdiely počítať aj priamo z meraných hodnôt. Z podobnosti trojuholníkov vyplýva
Pre jeden súradnicový rozdiel platí
a analogicky pre druhý súradnicový rozdiel
Zlomky vo vzorcoch (2.15) a (2.16) majú pre jednu rovnakú priamku konštantné hodnoty
yx-yP/dm=k xK-xP/dm=k (2.17) d
Potom pre súradnicové rozdiely bodov na meračskej priamke možno napísat nasledujúce vzorce
(2.18)
Postupným sčítaním jednotlivých súradnicových rozdielov vypočítame súradnice meračských bodov P,, Pz, ..., ktoré už pokladáme za vyrovnané. Na konci zistené súradnice bodu K sa musia presne zhodovaf s danými súradnicami, čo je kontrolou správnosti výpočtu.
(2.19)
2.6 ZISŤOVANIE CENTRAČNÝCH PRVKOV A VÝPOČET CENTRAČ
NÝCH ZMIEN SMEROVVplyvom počasia, a tým aj deformáciou stavebného materiálu, signály na trigonometrických alebo zhusťovacích bodoch nezostanú dlhší čas v nezmenenej polohe (aj keď pôvodne boli postavené zvislo nad stredom krížika stabilizačnej značky). Preto treba na umelo signalizovaných bodoch pred každým meraním zisťovať správnosť polohy signálov. Niekedy treba pri meraní zvoliť excentricky aj stanovisko prístroja. ak sú v zámerách prekážky.
Pretože smery merané z excentrického stanoviska alebo na excentrické ciele nereprezentujú správne hodnoty smeru z centra jedného bodu do centra druhého, musia sa redukovať na správne hodnoty. Zmeny, o ktoré sa nesprávne excentrické hodnoty opravujú, sa nazývajú centračné zmeny. Určujú sa z centračnýc
h prvkov, ku ktorým patrí:- excentricita e; je to vodorovná vzdialenosť excentra E od centra C. - centračný uhol E; je to meraný alebo určený smerník na centre C od smeru excentricity EC v smere pohybu hodinových ručičiek na zameriavaný bod P,
- dĺžka d, je vzdialenosť b
odu C od bodu P, na ktorý sa meria excentrický smerník.Označovanie centračných prvkov
Center, t.j. stabilizovaná poloha geodetického bodu označuje sa Q.
Stanovisko, na ktorom stojí prístroj, označuje sa krúžkom Q. Cieľ sa označuje +.
Vzáj
omný vzťah medzi centrom, stanoviskom a cieľom trigonometrického bodu môže byť takýto :1. Stanovisko aj cieľ sú centrické.
2. Stanovisko je centrické, cieľ je excentrický.
3. Cieľ je centrický, stanovisko je excentrické.
4. Stanovisko je excentrické, cie
ľ je excentrický, pričoma) cieľ môže byť totožný so stanoviskom,
b) cieľ nie je totožný so stanoviskom.
2.6.1 Výpočet centračných zmien smerov
na dostredenie cieľa, keď stanovisko je centrické (obr. 2.17), (tab. 2.3)
Postup výpočtu centračného uhla ε
a
k a<2R ε=2R-aak a>2R ε=4R-a
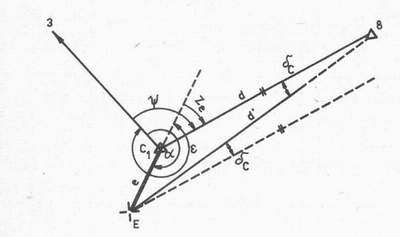
Obr. 2.17. Výpočet centračných zmien na excentrický cieľ
Ak bodom E vedieme rovnobežky so stranou d, vznikne uhol Ze aj pri bode E. Uhol oproti strane d je (Ze =). Pre malé excentricity bude malý aj uhol δc, z čoho vyplýva, že (Ze -) = Ze.
Pri veľkej excentricite treba uhol δc vypočítať aproximáciou. Ak e < eI, na výpočet použijeme približný vzorec
a výpočet prekontrolujeme graficky.
Ak eI < e < eII, použij
eme vzorec na druhú aproximáciuNa výpočet druhej aproximácie použijeme osnovu smerov opravenú o hodnoty δcI z prvej aproximácie, ktoré berieme s opačným znamienkom.
Ak eII < e, δc sa
vypočíta podľa presného vzorca - riešením trojuholníka sínusovu vetou.
Pre V. rád ČSTS platia tieto hodnoty: eI = 2,2 m, eII = 16,4 m.
2.6.2 Výpočet centračných zmien smerov na dostredenie stanoviska aj cieľa
V praxi môžu nastať dva prípady
:1. Stanovisko je zhodné s cieľom
Vypočítame uhol ε = 4R - a (obr. 2.18), (tab. 2.4 ). Tento uhol pripočítame k meraným smerom osnovy ψ', čím dostaneme smery Ze, orientované od smeru excenter - center (EC). Centračné zmeny δ
c (ak e < eI) vypočítame zo vzorca(2.82)
a prekontrolujeme graficky.
Ak eI < e < eII, počítajú sa centračné zmeny podľa presného vzorca
a prekontrolujú sa podľa približného vzorca.
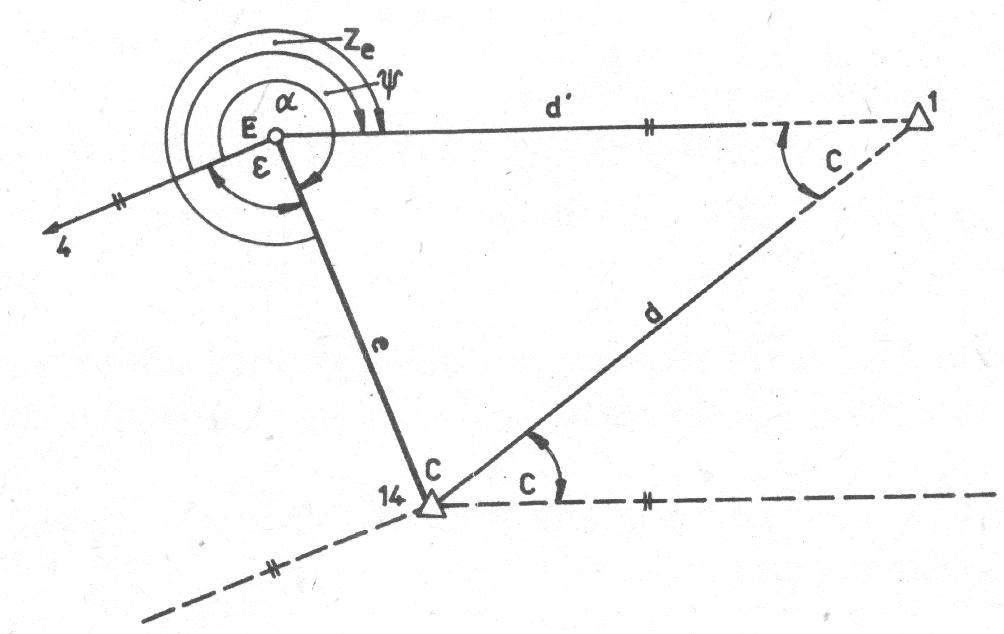
Obr. 2.18. Výpočet centračných zmien na dostredenie stanoviska a cieľa
Ak je excentrické stanovisko totožné s cieľom a excentricita e je malá, potom redukcia na stred je totožná s redukciou na cieľ pre opačnú zámeru. V týchto prípadoch sa nepočítajú centračné zmeny na dostredenie cieľa. Pri veľkých excentricitách nemôžeme prepísať centračné zmeny na stred ako centračné zmeny na cieľ k opačným zámerám.
2. Stanovisko nie je totožné s cieľom
Výpočet sa rozdeľuje na dve časti:
a) Vypočítajú sa centračné zmeny na dostredenie stanoviska. Centračnými prvkami
sú excentricita e' a uhol τ.b) Meraná osnova smerov sa redukuje na stred a vykoná sa redukcia na cieľ. Centračnými prvkami sú excentricita e a pripájací uhol α
= β+ γ (obr. 2.19).Uhly ω a β sa merajϊ
, uhol y sa vypočíta pomocou sínusovej vetyPoznámka: V
ýpočet centračných zmien smerov na dostredenie stanoviska, ak cieľ je centrický, je rovnaký ako výpočet vtedy, keď cieľ je totožný s excentrickým stanoviskom (pozri tab. 2.4 ).Centračné zmeny sa graficky kontrolujú nomogramom (tab.2.5 ),
zostrojeným podľ
a rovnicePresnosť určenia centračných prvkov
Presnosť výpočtu centračnej zmeny môžeme meniť použitím približného alebo presného vzorca na jej výpočet.
Skutočná geometrická presnosť centračnej zmeny závisí od presnosti určenia centračný
ch prvkov e, ε, a d. Ak sa tieto veliθiny určili nepresne, centračná zmena určená aj presným výpočtom nie je presná.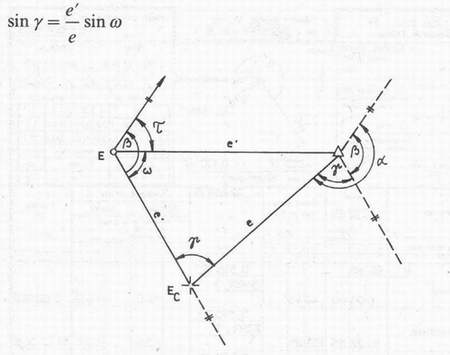
Obr. 2.19. Výpočet centračných zmien
Pri jej výpočte vyjdeme zo vzťahu
kde e, ε, d sϊ
nezávislo premenné hodnoty.Výsledná chyba
∆δcc bude daná súčtom čiastkových chýb jednotlivých premennýchVšeobecne sa vyžaduje, aby pre stredné pomery v trigonometrickej sieti (t.j. d > 500 m, e < 1 m) centračné prvky sa určili takto:
- excentricita e s presnosťou na milimeter,
- uhol s s presnosťou na minútu,
- dĺžka d s presnosťou na jeden meter.
Keď e < 20 m, stačí ju merať dvakrát, keď e > 20 m, treba ju merať aspoň trikrát. Keď sa vyskytne excentricita menšia ako 5 mm, možno ju zanedbať, pretože centračné zmeny pre takúto excentricitu a bežné pomery v trigonometrickej sieti budú pod hranicou meračských chýb.
Od veľkosti excentricity závisí aj presnosť meraného uhla ε
.Ak e < 1 cm, stačí uhol ε merať na 1°
e < 10 cm
, stačí uhol ε merať na 10' ,e < 1 m, stačí uhol ε merať na 1' ,
e < 10 m, stačí uhol ε merať na 10"
e < 100 m, stačí uhol ε merať na 1".
Presnosť určenia dĺžky trigonometrickej strany d závisí od veľkosti samotnej dĺžky d a od veľkosti exc
entricity e.Pre najnepriaznivejší prípad e = 90° alebo 270°, e = 1 m a
di = 1 km, treba poznať di s presnosťou 48 cm,
di = 2 km, treba poznať di s presnosťou 1,94 m,
di = 3 km, treba poznať di s presnosťou 4,36 m,
pre e=lOm a
di = 1 km, treba poznať di s presnosťou
5 cm,di = 2 km, treba poznať di s presnosťou 19,4 cm,
di = 3 km, treba poznať di s presnosťou 44 cm,
všetko pre prípady, ak vyžadovaná presnosť v centračnej zmene δ má byť 0,1".
Ak nemusíme, potom s excentricitami nerátame.
2.7 URČOVANI
E PRAVOUHLÝCH SÚRADNÍC BODOV Z MERANÝCH SMEROVMedzi najpoužívanejšie postupy geodetických metód určovania polohy bodov patrí pretínanie na jeden bod (pretínanie napred a pretínanie nazad).
Súradnice neznámeho bodu pretínaním napred zo známych bodov možno určiť rozličnými postupmi.(viac nájdete v predmete geodetické výpočty.)